Phoresis and Stokesian hydrodynamics
Phoresis and Stokesian hydrodynamics of active and driven particles
- About
- Controlled optofluidic crystallization of colloids tethered at interfaces
- Periodic orbits of active particles
- Crystallization at a plane no-slip surface
- Flow-induced phase separation is controlled by boundary conditions
- Autophoretic arrest of flow-induced phase separation
- Active particles in external potentials
- Electrohydrodynamic flows: self-assembly of nanoparticles
About
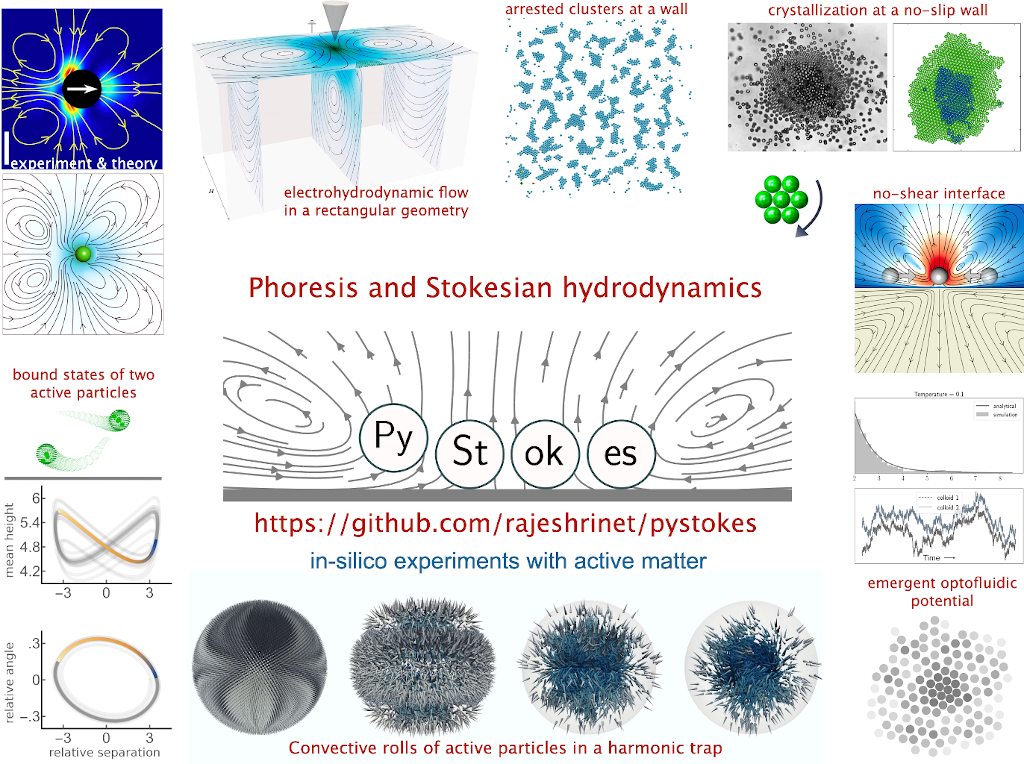
In this blog, I describe a theory for studying phoretic and hydrodynamic interactions of colloidal particles. The main focus is to understand these long-ranged interactions for a new class of colloids, called active particles, which are distinguished by their ability to produce flow, and thus motion, in the absence of external forces or torques. Active particles can create flow - even when stationary - due to large surface gradients from local nonequilibrium processes. These nonequilibrium processes may be due to the motion of cilia, as in microorganisms (Brennen & Winet, 1977) or osmotic flows of various kinds in response to spontaneously generated gradients of phoretic fields (Ebbens & Howse, 2010) at the colloidal particle. The latter, often called autophoresis, is a generalisation of well-known phoretic phenomena including, inter alia, electrophoresis (electric field), diffusiophoresis (chemical field) and thermophoresis (temperature field) that occur in response to externally imposed gradients of phoretic fields (Anderson, 1989).
Hydrodynamic and phoretic interactions between active particles in a viscous fluid are central to the understanding of their collective dynamics. Under experimentally relevant conditions, the motion of the fluid is governed by the Stokes equation and that of the phoretic field, if one is present, by the Laplace equation. The “activity” appears in these equations as boundary conditions on the particle surfaces that prescribe the slip velocity in the Stokes equation and flux of the phoretic field in the Laplace equation. The slip is a mechanism to drive fluid flow in absence of any external forces and torques.
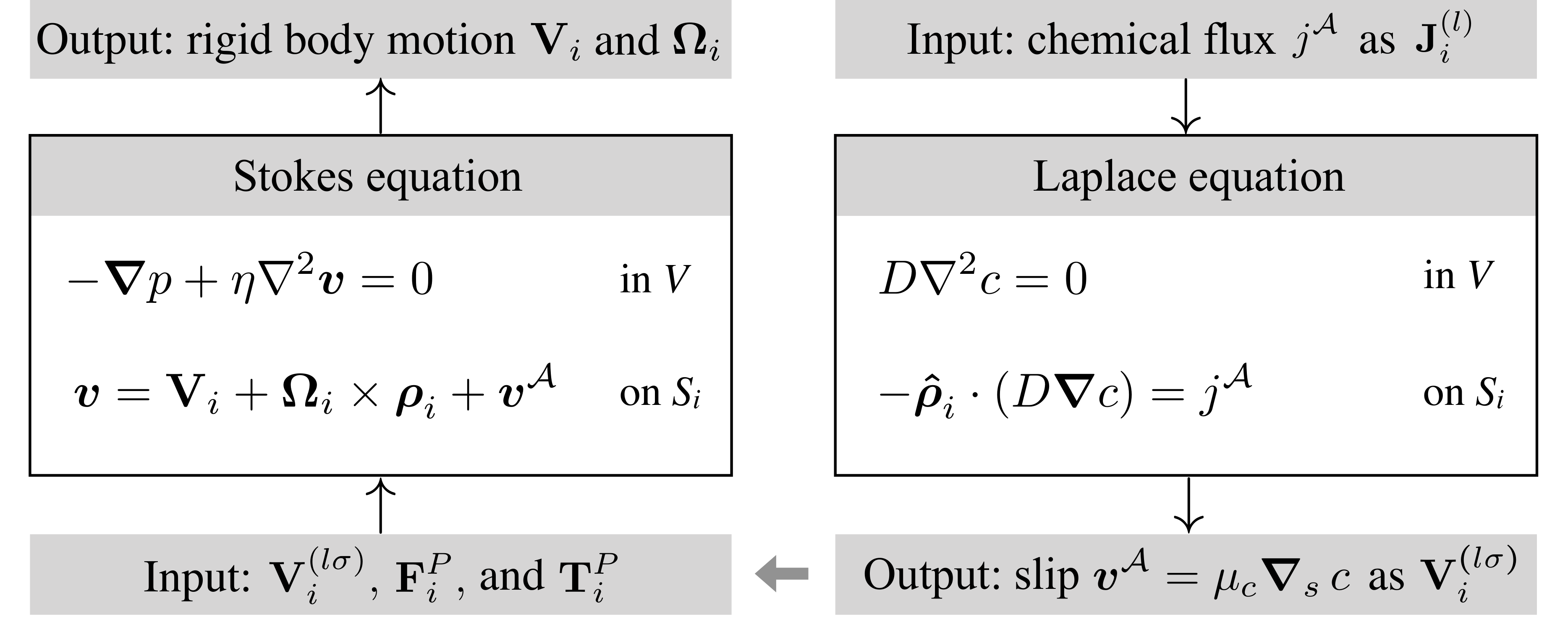
We model an active particle as a spherical colloidal particle with surface slip. Thus, the theory is applicable to both active and driven particles. The slip velocity and the phoretic flux are related by a linear constitutive law that can be derived from a detailed analysis of the boundary layer physics (Anderson, 1989). The Stokes and Laplace equations are coupled by this linear constitutive law only at the particle boundaries. The linearity of the governing equations and the coupling boundary conditions allows for a formally exact solution of the problem of determining the force per unit area on the particle surfaces. This formally exact solution can be approximated to any desired degree of accuracy by a truncated series expansion in a complete basis of functions on the particle boundaries. This, in turn, leads to an efficient and accurate numerical method for computing hydrodynamic and phoretic interactions between active particles. We solve these equations simultaneously - using a grid-free method, combining the integral representation of Laplace and Stokes equations, spectral expansion, and Galerkin discretization - to compute phoretic and hydrodynamic interactions between spheres with slip boundary conditions on their surfaces. Details are available in Singh and Adhikari JPC 2018 and Singh, Adhikari and Cates JCP 2019
The above formalism has been implemented in a numerical library, PyStokes. PyStokes is a numerical library for phoresis and Stokesian hydrodynamics in Python. The resulting methodology has been applied to study various experimental phenomena of recent interest in active and driven matter. In what follows, a selected list of applications is presented.
Controlled optofluidic crystallization of colloids tethered at interfaces

The interplay between laser light, trapped particles, and fluid flow can produce counterintuitive effects in optical tweezing. Here we uncover an attractive, long-ranged, non-equilibrium force field centered on an optically trapped particle near a water-oil interface, produced by local heating and mediated by global fluid flow. This causes surrounding untrapped colloids, tethered to the interface but allowed to diffusely freely along it, to crystallize around the force center. In this configuration, the non-equilibrium force is the gradient of a potential, of strength proportional to the local heating, which, surprisingly, allows for an effective equilibrium description. Our results open unexplored routes to optofluidic manipulation and assembly of colloidal particles.
See also this synopsis: Small Spheres Freeze When Hot
Periodic orbits of active particles
Reference: A Bolitho, R Singh, R Adhikari, Physical Review Letters 124 (8), 088003 (2020)

Our work shows that the oscillatory dynamics of a pair of active particles near a boundary, best exemplified by the fascinating dance of the green algae Volvox, can be understood in terms of Hamiltonian mechanics, even though the system does not conserve energy. At the heart of this dance, which is a limit cycle of a dynamical system, is a Hamiltonian, damped by gravitational torque and driven by fluid flow reflected off the boundary. For small oscillations, this Hamiltonian is identical to that of a pendulum and, like a metronome, sets the beat of the dance. For large oscillations, the beat can be evaluated with the same mathematics as for a pendulum, and when damping and driving are taken into account, agrees very well with experiment. This establishes without doubt that the enigmatic Volvox dance, rather than being an evolutionarily selected biological phenomenon, is a physical phenomenon that can be understood fully in terms of the familiar concepts of mechanics. Our study highlights the significance of fluid flows and their distortion by boundaries in active matter and shows that the applicability of Hamiltonian mechanics extends beyond its intended domain of energy-conserving systems to time-irreversible, dissipative, active systems.
Crystallization at a plane no-slip surface
Reference: R Singh, R Adhikari, Physical Review Letters 117, 228002 (2016)
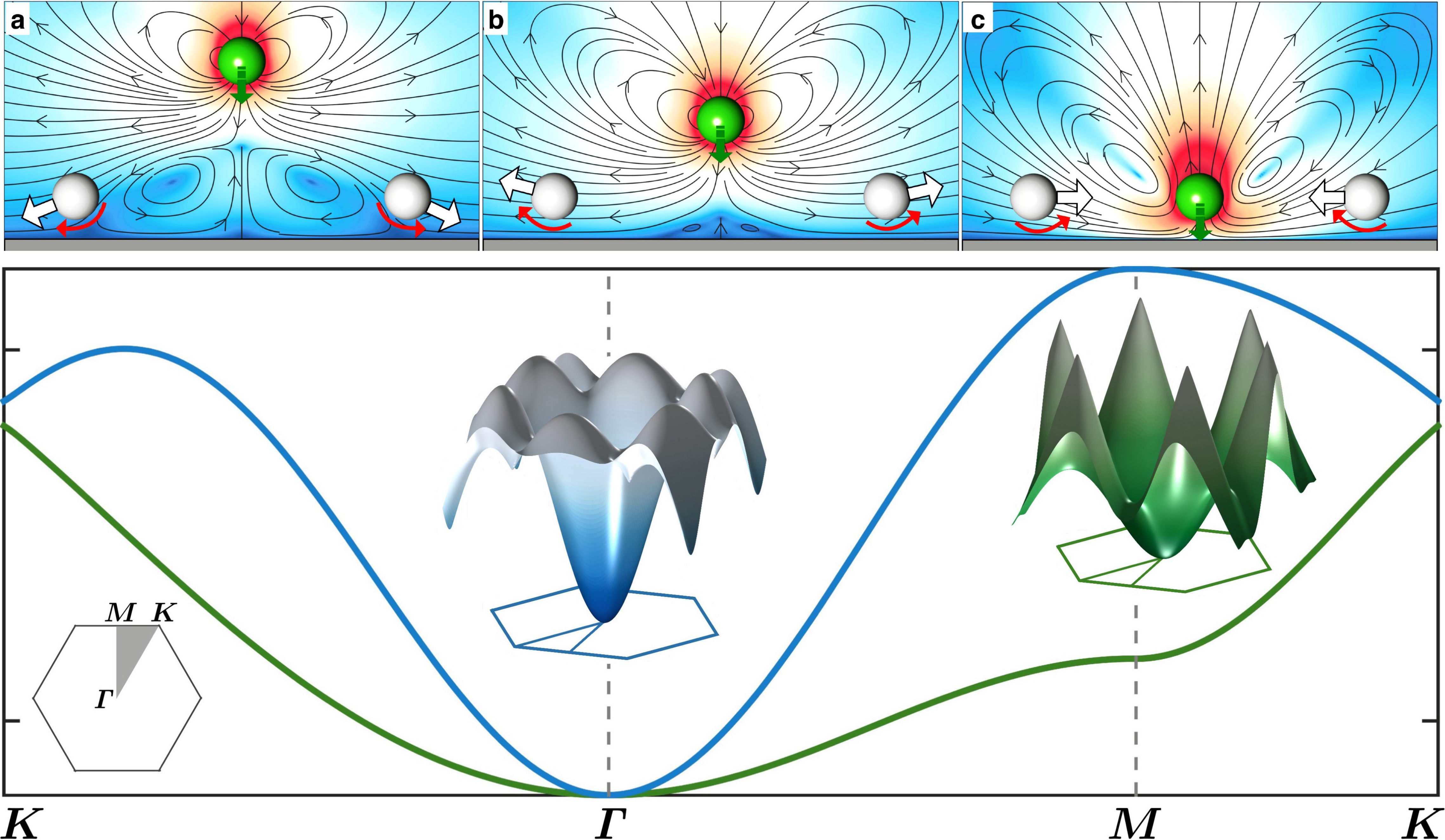
It is well-known that crystallization of colloids approximating hard spheres is due, paradoxically, to the higher entropy of the ordered crystalline state compared to that of the disordered liquid state. Out of equilibrium, no such general principle is available to rationalize crystallization. Here, we identify a new non-equilibrium mechanism, associated with entropy production rather than entropy gain, which drives crystallization of active colloids near plane walls. This is a new mechanism of spontaneous symmetry breaking, with no analogue in equilibrium. The properties of the non-equilibrium crystal, consequently, show remarkable exceptions: strong dissipation suppresses propagating phonon-modes and turns them diffusive, yet, activity enhances the elastic moduli of the crystal. An active crystal, then, has reduced phase fluctuations and is less susceptible to the destruction of long-ranged order, even though it is two-dimensional. The investigation of topological phase transitions in these systems presents, therefore, exciting avenues for future research. There is an excellent qualitative and quantitative match of our results with two recent experiments.
Kinetics of crystallization
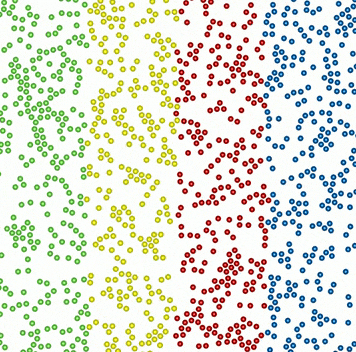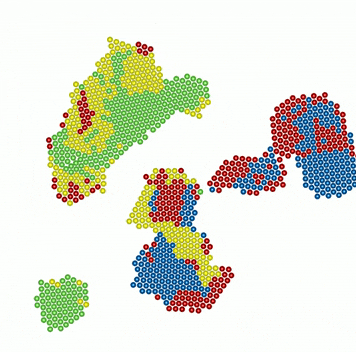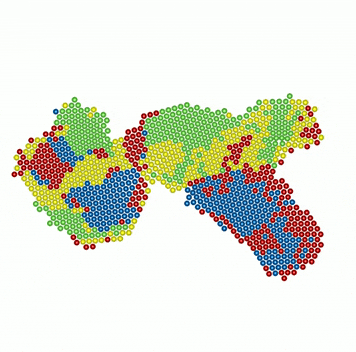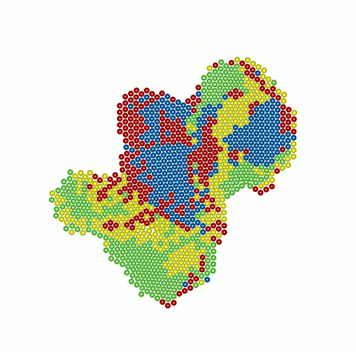
Attractive monopolar flow of active particles near a plane surface
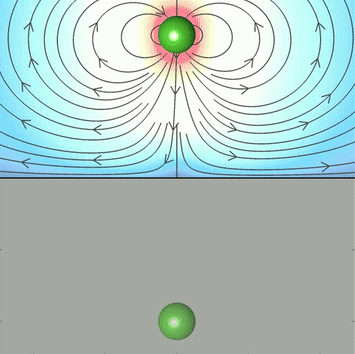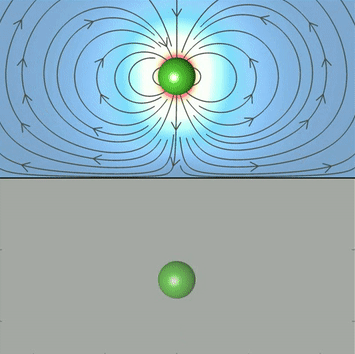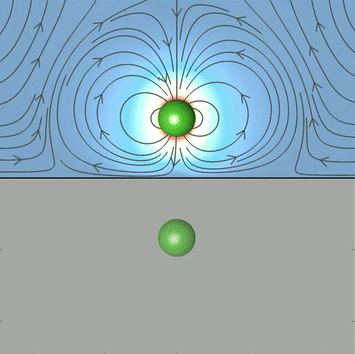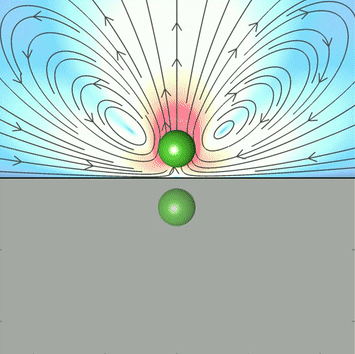
Self-assembly of hexagonal cluster of active particles

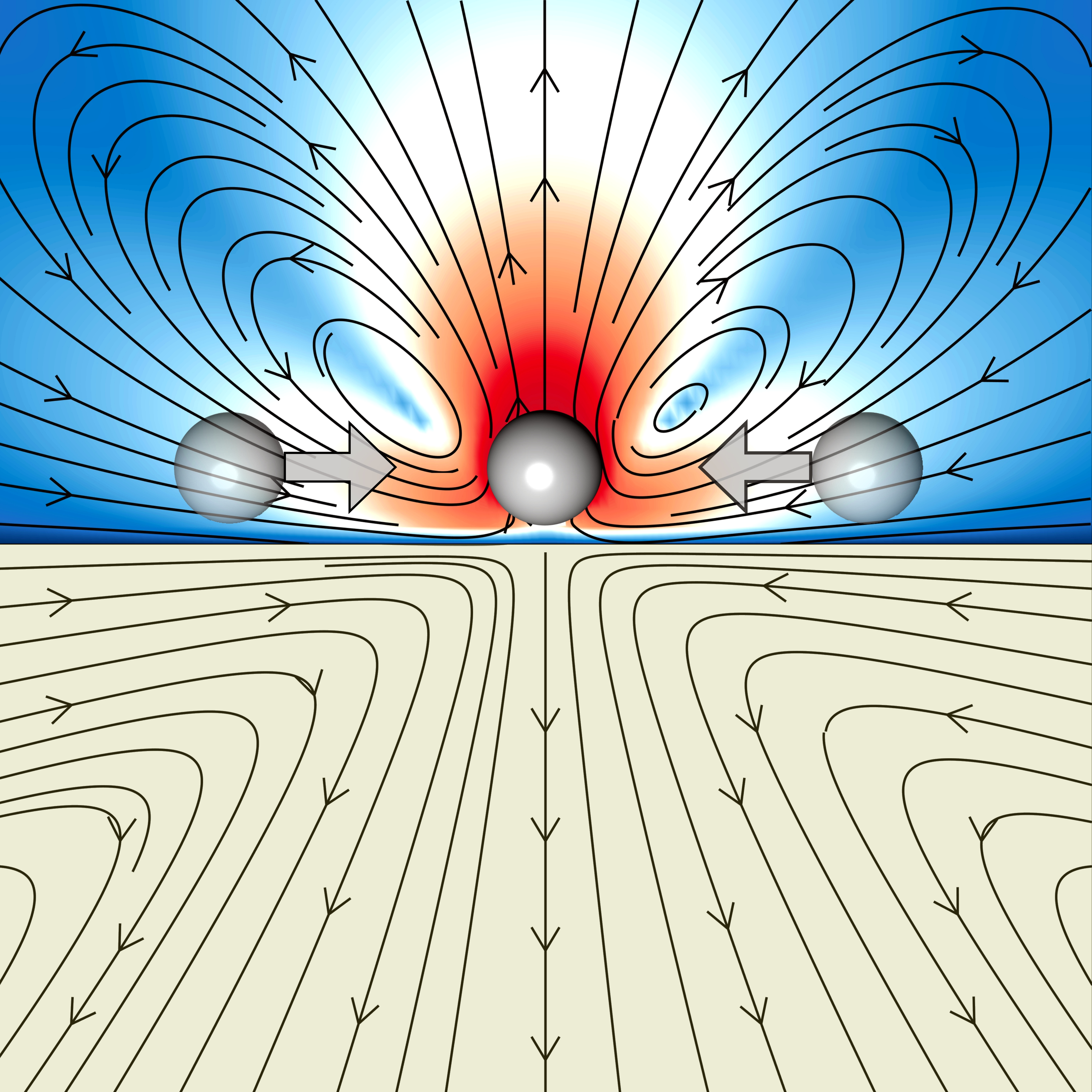
Flow-induced phase separation is controlled by boundary conditions
Active colloids - microorganisms, synthetic microswimmers, and self-propelling droplets - are known to self-organize into ordered structures at fluid-solid boundaries. Their mutual entrainment in the attractive component of the flow has been postulated as a possible mechanism underlying this phenomenon. In this work, we describe this fluid-induced phase separation by combining experiments, theory, and numerical simulations, and demonstrate its control by changing the hydrodynamic boundary conditions. We show that, for flow in Hele-Shaw cells, metastable lines or stable traveling bands of colloids can be obtained by varying the cell height, while for flow bounded by a plane, dynamic crystallites are formed. At a plane no-slip wall, these crystallites are characterized by a continuous out-of-plane flux of particles that circulate and re-enter at the crystallite edges, thereby stabilizing them, while the crystallites are strictly two-dimensional at a plane where the tangential stress vanishes. These results are elucidated by deriving, using the boundary-domain integral formulation of Stokes flow, exact expressions for dissipative, long-ranged, many-body active forces and torques between them in respective boundary conditions. The resulting numerical simulations of motion under the action of the active forces and torques are in excellent agreement with experiments. Our work demonstrates the control of phase separation of active particles by boundary conditions.
Vortex-stabilised crystallites at a plane no-slip surface

Two-dimensional crystallites at a plane no-shear surface

Traveling bands in a Hele-Shaw cell


Autophoretic arrest of flow-induced phase separation
Reference: R Singh, R Adhikari, ME Cates, The Journal of Chemical Physics 151, 044901 (2019)
Recent experiments have reported the arrest of phase separation in a suspension of active colloids at a plane wall. Attractive hydrodynamic forces are known to cause the aggregation of active colloids at a plane wall. This flow-induced phase separation, in absence of any other interactions, drives the system to a complete phase separation. Here, we describe the role of chemical interactions in modifying this flow-induced phase separation of active colloids at a plane wall. We derive chemohydrodynamic forces and torques on colloids in the limit of rapid diffusion and slow viscous flow. We find that near a plane wall, these forces can be expressed as a gradient of a non-equilibrium potential. This potential can be varied from being purely repulsive to purely attractive by tuning the chemical activity of the colloids. The arrest of phase separation can then be understood from the emergence of a barrier in the effective potential.

Active particles in external potentials
The simplest system in which an interplay of non-uniform external fields, activity and Brownian motion can be studied is an active colloid confined in a three-dimensional harmonic potential. We consider two examples: (a) active particles in a single trap, and (b) active particles in a lattice of harmonic traps (optical lattice).
Non-equilibrium convective rolls of confined active particles in a single harmonic trap

Dynamics in an optical lattice
Reference: R Singh, R Adhikari, Journal of Physics Communications 2, 025025 (2018)
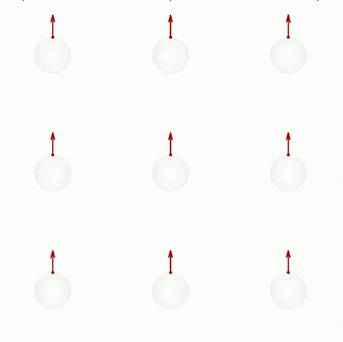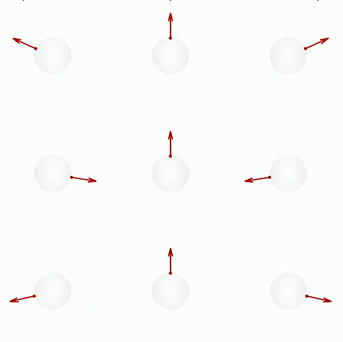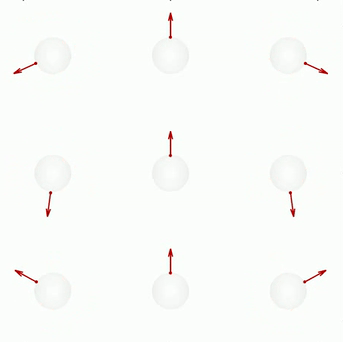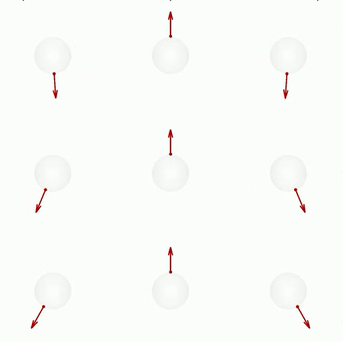
Dynamics of 1024 contractile and extensile active colloids in a spherical confinement
Reference: R Singh, R Adhikari, Journal of Physics Communications 2, 025025 (2018)
In this examples we consider apolar particles confined in a sphere. We show that the dynamics is different for contractile and extensile particles respectively.
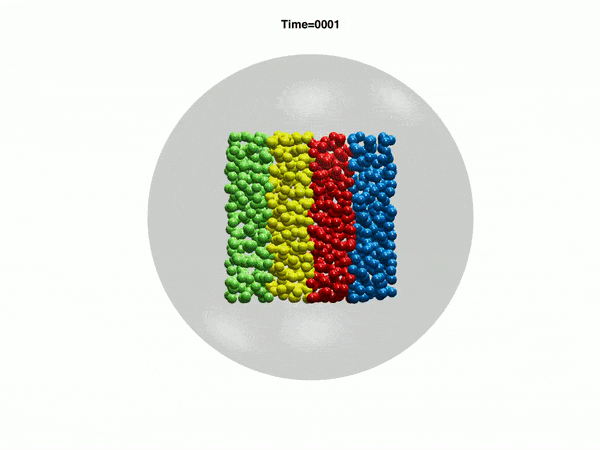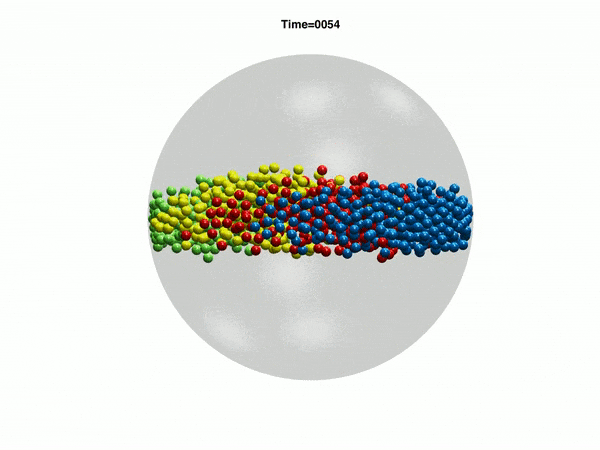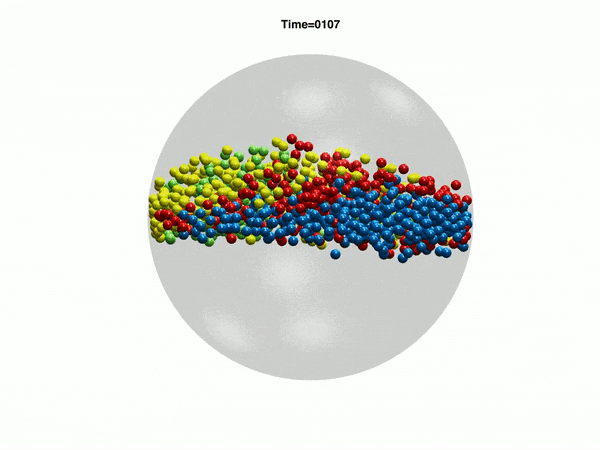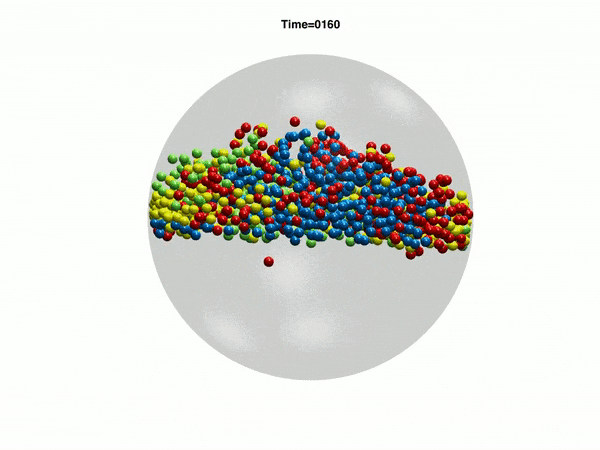
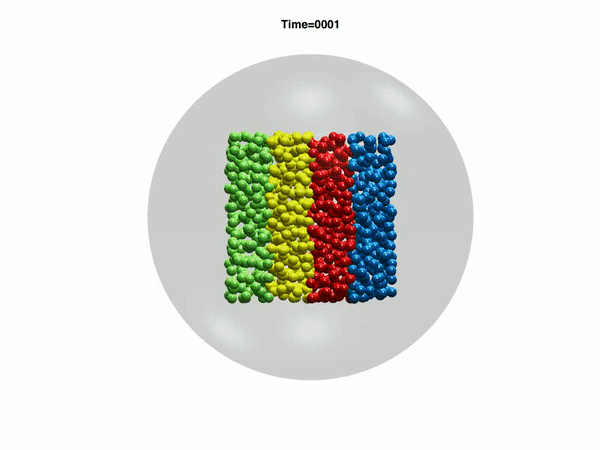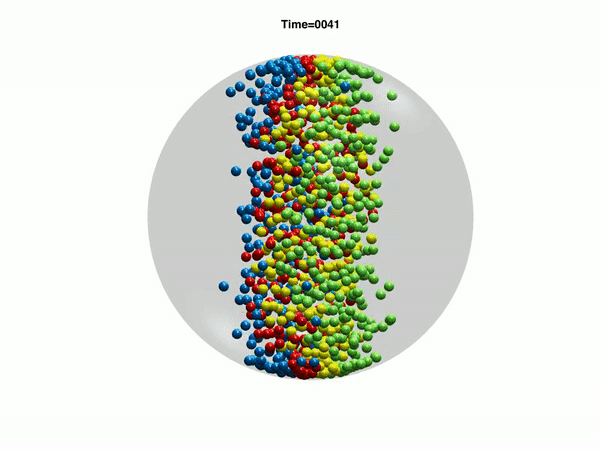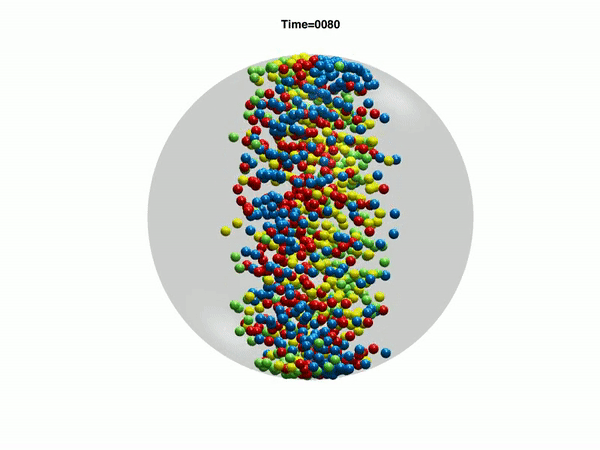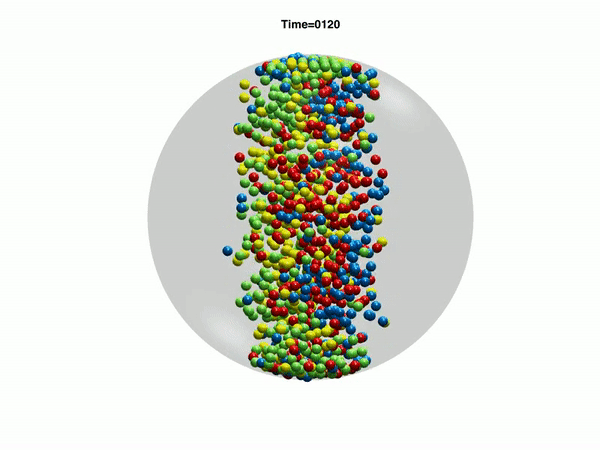
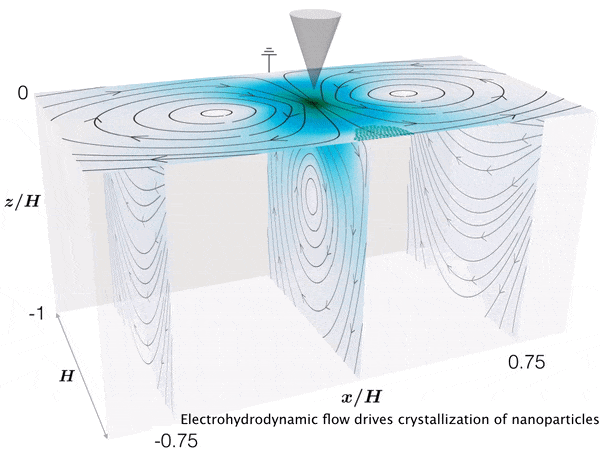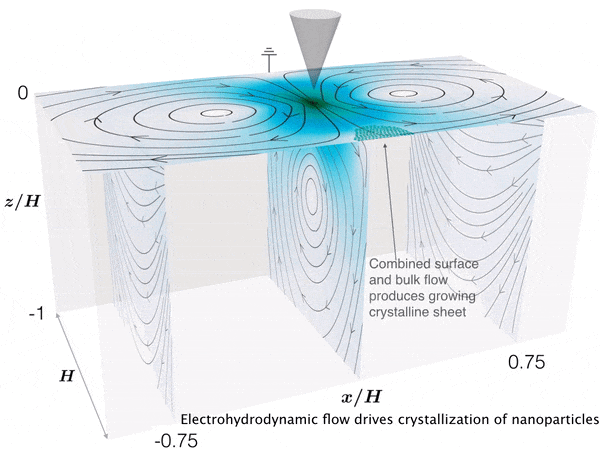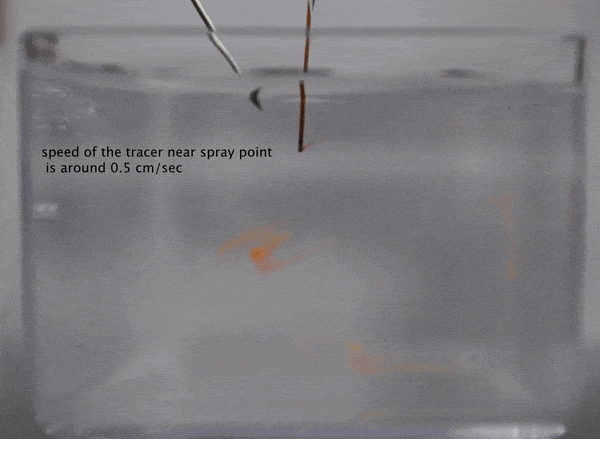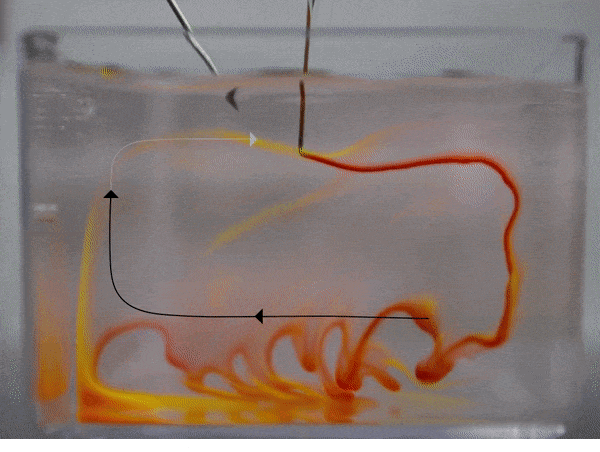
Electrohydrodynamic flows: self-assembly of nanoparticles
In the work, we consider a suspension of driven particles. Unlike an active colloid, a driven colloid can move only under the effect of external potentials. Here, we study the motion of particles under electrohydrodynamic flow in a rectangular geometry. Electrohydrodynamics is the study of the effects of electrostatic forces on fluid flow. Electrohydrodynamic flows result from the motion of free charges on the surface of a fluid by application of a tangential electric field along with the container (Melcher and Taylor, Annu Rev Fluid Mech 1969). In our case, free charged ions are sprayed using electrospray on the air-liquid interface of a rectangular container with an electrode, which provides a tangential electric field. The spray from the cone deposits charges at the air-liquid interface which is then set into motion by the tangential electric field due to the electrode. Thus, the formation of nanoparticle-nanosheet (NP-NS) is observed at the air-liquid interface.