Active scalar field theory
Statistical field theory without time-reversal symmetry
In this blog, an active scalar field theory with mass and momentum conservation has been used to rationalize recent experimental phenomena in nonequilibrium statistical physics.
Splitting active droplets
Microphase separation (phase separation arrested to a length-scale) is often observed in suspensions of spherical active particles. In such suspensions, the scalar concentration is the only order parameter, when there is no orientational order in the bulk. We show that such microphase separations can be achieved by extending theories of passive binary mixtures (for example, phase separation of oil droplets in passive binary oil-water mixtures). In thermal equilibrium systems, phase separation is a thermodynamic process where a uniformly mixed state can lower its free energy by dividing into phases. Ostwald ripening (small droplets disappear and bigger droplets grow) drives thermal equilibrium systems to full phase separation. In this blog, we show that by coupling the scalar density to fluid flow, the negative mechanical tension of an active suspension creates, via a self-shearing instability, a steady-state life cycle of droplet growth interrupted by division whose scaling behavior we predict.

The starting point in this theory is the diffusive dynamics of a conserved scalar field $\phi(\boldsymbol{r},t)$ in a momentum-conserving fluid of velocity $\boldsymbol{v}(\boldsymbol{r},t)$: $ \dot{\phi}+\boldsymbol{\nabla}\cdot\boldsymbol{J}+\boldsymbol{v}\cdot\boldsymbol{\nabla}\phi=0. $ Here, $\boldsymbol{J}$ is the current density of $\phi$, which obeys $ \boldsymbol{J}=-M \boldsymbol{\nabla}\frac{\delta\mathcal{F}}{\delta\phi} + \sqrt{2DM}\boldsymbol{\Lambda}, $ where $M$ is a mobility, $\boldsymbol{\Lambda}$ is a zero-mean, unit-variance Gaussian white noise, and $D$ is a noise temperature, while $\mathcal{F}$ is the Landau-Ginzburg free energy functional: $ \mathcal{F}[\phi]=\int\left(\frac{a}{2}\phi^{2}+\frac{b}{4}\phi^{4}+\frac{\kappa}{2}(\boldsymbol{\nabla}\phi)^{2}\right)d\boldsymbol{r}. $ This free energy functional admits bulk phase separation for $a<0$, with $b,\kappa>0$ for stability [Chaikin and Lubensky(2000)].
The fluid will be set into motion if the interfaces are not flat. The fluid flow, in the limit of low Reynolds number, is obtained from the solution of the Stokes equation: $\boldsymbol{\nabla}\cdot\boldsymbol{\sigma}=-\boldsymbol{f}$ with $\boldsymbol{f}=\boldsymbol{\nabla}\cdot(\boldsymbol{\Sigma}^{E}+\boldsymbol{\Sigma}^{A})$. Here $\boldsymbol{\sigma}=-p\boldsymbol{I}+\eta(\boldsymbol{\nabla}\boldsymbol{v}+(\boldsymbol{\nabla}\boldsymbol{v})^{T})$ is the Cauchy fluid stress, $\eta$ is viscosity, $\boldsymbol{I}$ is the identity tensor, and $p$ is the pressure field which contains all isotropic terms and ensures incompressibility $(\nabla\cdot\boldsymbol{v}=0)$. The deviatoric stresses in the bulk are due to gradients of the field $\phi$. Their explicit forms are: $\boldsymbol{\Sigma}^{E}=-\kappa\boldsymbol{S}$ and $\boldsymbol{\Sigma}^{A}=-(\tilde{\kappa}-\kappa)\boldsymbol{S}$, with $\boldsymbol{S}=(\boldsymbol{\nabla}\phi)(\boldsymbol{\nabla}\phi)-\tfrac{1}{d}|\boldsymbol{\nabla}\phi|^{2}\boldsymbol{I}$ in $d$-dimensions.
In the absence of $\boldsymbol{\Sigma}^{A}$, the above scalar field theory with mass and momentum conservation is called model H. With the addition of the active stress $\boldsymbol{\Sigma}^{A}$, which does not belong to any free energy, we have obtained $active$ Model H. By construction, active model H does not respect time-reversal symmetry. The interfacial tension, without activity, $\gamma_0=\sqrt{-8\kappa a^{3}/9b^{2}}$, is modified to $\gamma_{v}=\tilde{\kappa}\gamma_0/{\kappa}$. A self-shearing instability is obtained for active extensile stress ($\gamma_v <0$) due to stretching of the interface from the resulting fluid flow (see below).
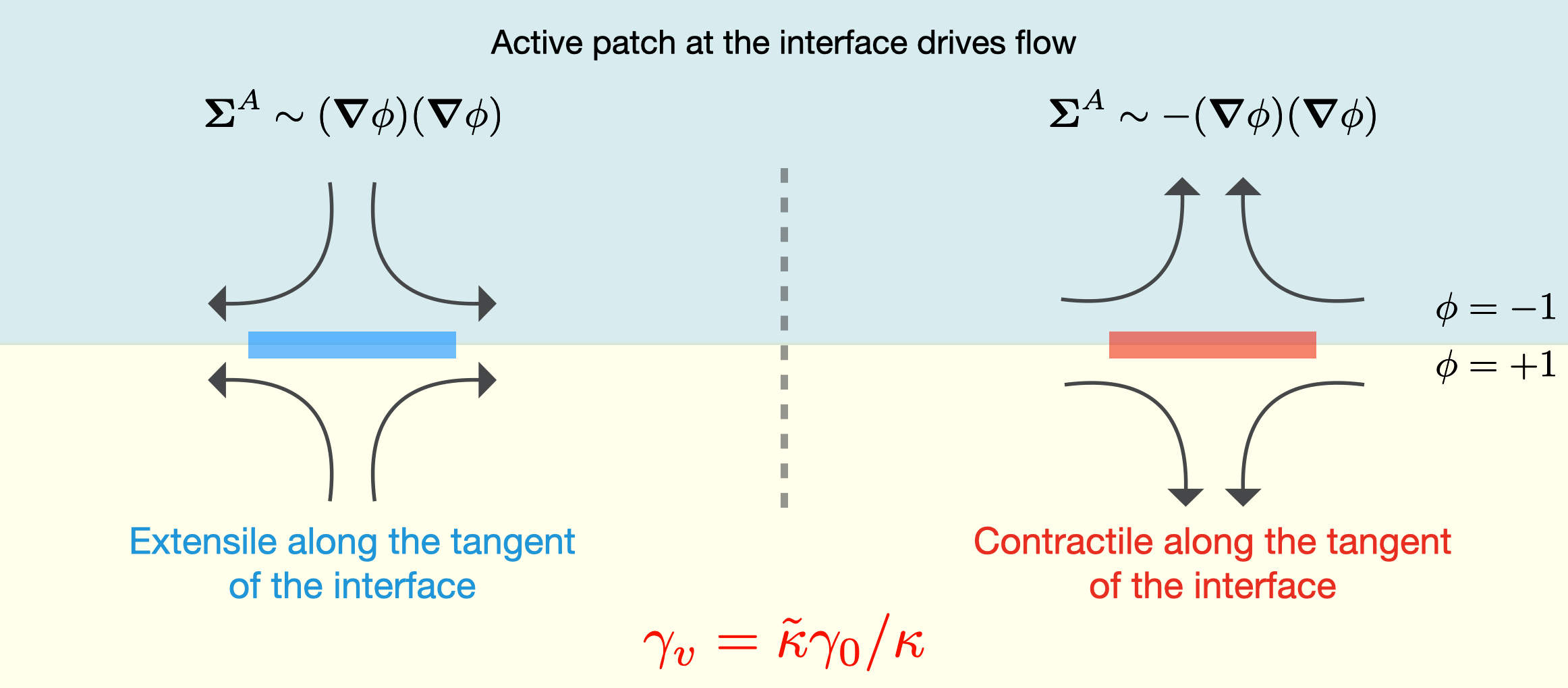
This instability interrupts the growth of droplets by splitting them. The extensile active stress has the effect of reversing the sign of the effective tension which arrests the growth. This is balanced by Ostwald ripening: small droplets evaporate while large ones grow until they in turn become unstable. The result is a dynamical steady state maintained by the self-shearing instability. We show that the typical length scale at steady state is proportional to the $1/\sqrt{\tilde{\kappa}}$. When the diffusive tension is also negative, this is replaced by an arrested regime (mechanistically distinct, but with similar scaling) where division of small droplets is prevented by reverse Ostwald ripening.
Reference: Rajesh Singh and Michael E. Cates. Phys. Rev. Lett. 123, 148005 (2019)
Self-propelling active droplets
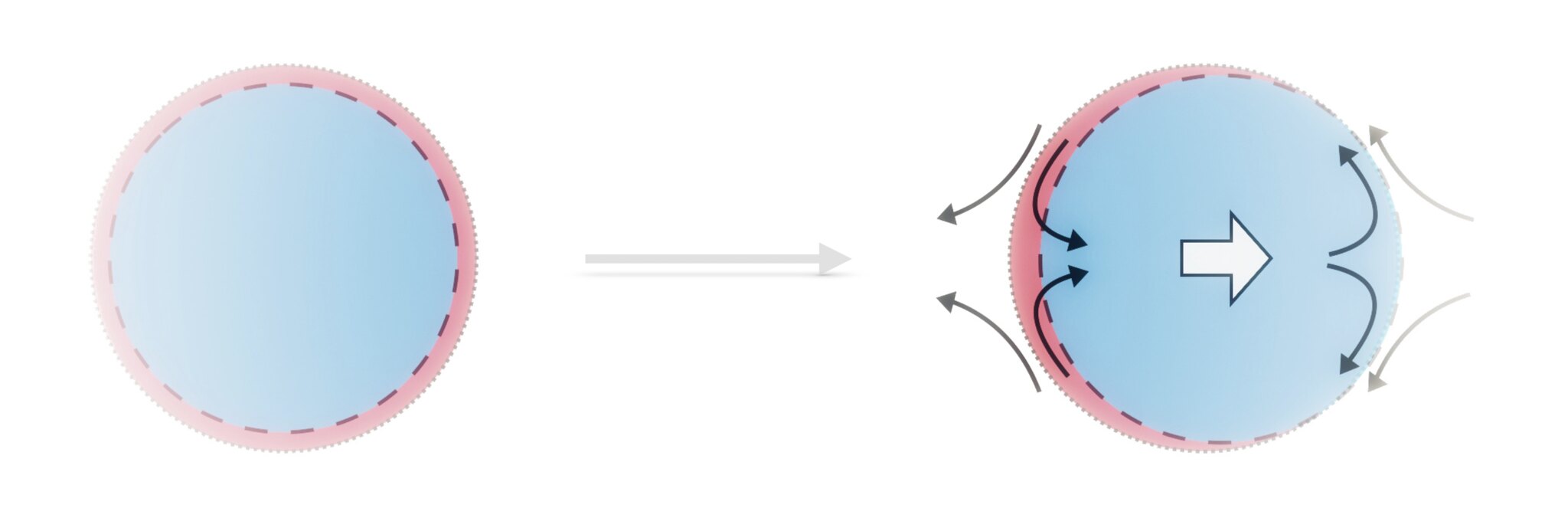
In this work, we present a model of self-propulsion in active droplets, such as cells, by extending the above theory to two scalar fields. The two scalar fields, in the case of a cell, represent the cytoplasm and a contractile cortex. An active stress couples the two scalar fields. The self-propulsion results from the activity when rotational symmetry is spontaneously broken. We find, both analytically and numerically, that the swimming speed does not depend on the radius of the droplet, while it varies linearly with the activity parameter and with the droplet area fraction.
I have also developed, PyGL, a numerical library for statistical field theory in Python. The library has been specifically designed to study field theories without time-reversal symmetry. The library constructs differentiation matrices using finite-difference and spectral methods. To study the role of momentum conservation, the library also allows computing fluid flow from the solution of the Stokes equation.
Reference: Rajesh Singh, Elsen Tjhung, and Michael E. Cates. Phys. Rev. Research 2, 032024(R) (2020)